The Basics

Symbols

The concept of symbols is similar to what is described in the SymPy tutorial. Symbols do not store actual numerical values; instead, they represent symbolic names or symbolic expressions. This allows for performing symbolic mathematical operations.

In NineToothed, you can create a symbol using the Symbol class. For example, in the code below, we first create two symbols named BLOCK_SIZE_M and BLOCK_SIZE_N, and then perform a multiplication operation on them:

>>> from ninetoothed import Symbol
>>> BLOCK_SIZE_M = Symbol("BLOCK_SIZE_M")
>>> BLOCK_SIZE_M
BLOCK_SIZE_M
>>> BLOCK_SIZE_N = Symbol("BLOCK_SIZE_N")
>>> BLOCK_SIZE_N
BLOCK_SIZE_N
>>> BLOCK_SIZE_M * BLOCK_SIZE_N
BLOCK_SIZE_M * BLOCK_SIZE_N

Symbolic Tensors

Similar to many deep learning frameworks, tensors are a core concept in NineToothed. However, tensors in NineToothed differ slightly from those in other frameworks—they do not store actual data. Instead, they store symbolic expressions in member variables such as shape and strides. For this reason, we refer to them as symbolic tensors.

In NineToothed, you can create a tensor using the Tensor class. As shown in the example below, Tensor(2) creates a 2-dimensional tensor—essentially, a matrix. Note that the shape member contains symbolic expressions rather than concrete values:

>>> from ninetoothed import Tensor
>>> x = Tensor(2)
>>> x.shape
(ninetoothed_tensor_0_size_0, ninetoothed_tensor_0_size_1)

Tensor-Oriented Metaprogramming

Thanks to symbolic tensors, we can perform certain compile-time operations on tensors in NineToothed. These operations are called meta-operations, such as tile, expand, squeeze, permute, and so on.

For example, in the following code, we apply the tile operation to x, which divides x into blocks of shape (BLOCK_SIZE_M, BLOCK_SIZE_N):

>>> x_tiled = x.tile((BLOCK_SIZE_M, BLOCK_SIZE_N))
>>> x_tiled.shape
((ninetoothed_tensor_0_size_0 - (BLOCK_SIZE_M - 1) - 1 + BLOCK_SIZE_M - 1) // BLOCK_SIZE_M + 1, (ninetoothed_tensor_0_size_1 - (BLOCK_SIZE_N - 1) - 1 + BLOCK_SIZE_N - 1) // BLOCK_SIZE_N + 1)
>>> x_tiled.dtype.shape
(BLOCK_SIZE_M, BLOCK_SIZE_N)

We notice that the dtype of x_tiled also has a shape attribute. This is because tensors in NineToothed can be nested—that is, the elements of a tensor can themselves be tensors.

In other words, during the tile operation, we create a two-level tensor: Each element of the outer tensor is itself an inner tensor. To make this easier to understand, let’s walk through a numerical example:

>>> BLOCK_SIZE_M = 2
>>> BLOCK_SIZE_N = 2
>>> x = Tensor(shape=(4, 8))
>>> x_tiled = x.tile((BLOCK_SIZE_M, BLOCK_SIZE_N))
>>> x_tiled.shape
(2, 4)
>>> x_tiled.dtype.shape
(2, 2)

As shown in the figure below, we’ve tiled the original tensor x of shape (4, 8) into blocks of shape (2, 2) (the inner tensors), resulting in a total of (2, 4) such blocks (the outer tensor):

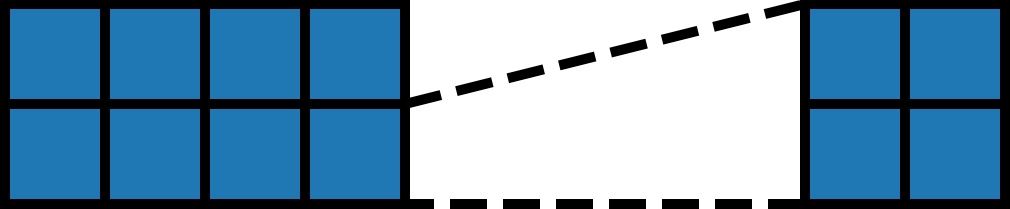
Arrange-and-Apply Paradigm

After introducing meta-operations, you should be able to understand what operations can be performed on individual tensors at compile time. A series of such operations is referred to as arrangement. However, this is not enough, as we also need to establish the relationship between multiple parameter tensors.

Such relationships are managed by the NineToothed compiler: The NineToothed compiler launches programs based on the shape of the outermost tensors of the arranged parameter tensors and maps the second outermost tensors to these programs.

We can understand this concept using a simple arrangement function:

def arrangement(x, y, z, BLOCK_SIZE=ninetoothed.block_size()):
    return x.tile((BLOCK_SIZE,)), y.tile((BLOCK_SIZE,)), z.tile((BLOCK_SIZE,))

In this function, we apply the tile operation to the vectors x, y, and z to divide each vector into blocks of size BLOCK_SIZE. For example, if each vector’s length is 16 and BLOCK_SIZE is 2, each vector can be divided into 8 blocks, with each block having a length of 2. The arranged x, y, and z would then look as follows:

Based on this arrangement, the NineToothed compiler will launch 8 programs and map the elements of the outermost tensors of the arranged x, y, and z (i.e., the second outermost tensors) to these 8 programs.

Now that we have these mappings, we can launch the programs accordingly. However, we are still one step away from fully implementing an algorithm, because we have not defined what each program should do. In other words, we need to define how to apply the arranged tensors. In NineToothed, this can be done by defining an application function.

For example, to define vector addition, we can create the following application function:

def application(x, y, z):
    z = x + y

The logic of the code is simple: It adds x and y and stores the result in z. However, it is important to note that the parameters of the application function are the elements of the outermost tensors of the arranged parameter tensors (i.e., the second outermost tensors), not the tensors themselves. That is, based on the above assumptions, x, y, and z here represent blocks of length 2, not the original tensors of length 16.

At this point, we have defined both the arrangement and application functions. The remaining task is to integrate them into a compute kernel. In NineToothed, we can use ninetoothed.make to achieve this:

kernel = ninetoothed.make(arrangement, application, (Tensor(1), Tensor(1), Tensor(1)))

This code means that we want to arrange three 1-dimensional tensors (vectors) according to the arrangement function, and apply the arranged tensors using the application function to form a compute kernel kernel. The paradigm of constructing a compute kernel this way is called the arrange-and-apply paradigm.

We can invoke kernel as follows:

import torch

dtype = torch.float16
device = "cuda"

x = torch.tensor((1, 2, 3), dtype=dtype, device=device)
y = torch.tensor((4, 5, 6), dtype=dtype, device=device)

z = torch.empty_like(x)
kernel(x, y, z)

reference = torch.tensor((5, 7, 9), dtype=dtype, device=device)
assert torch.allclose(z, reference)

As shown, when we call kernel, we do not provide an actual value for BLOCK_SIZE. This is because when constructing BLOCK_SIZE, we used ninetoothed.block_size, which represents that we want to use the configurations generated by the NineToothed compiler for auto-tuning. If we want to provide a value manually (for example, during debugging), we can directly assign a specific value as follows:

def arrangement(x, y, z, BLOCK_SIZE=1024):
    return x.tile((BLOCK_SIZE,)), y.tile((BLOCK_SIZE,)), z.tile((BLOCK_SIZE,))

Indexing and Iteration

Through the vector addition example, we got a brief understanding of how to develop compute kernels using NineToothed. In that example, the parameter tensors were arranged into two-level tensors. However, tensors in NineToothed are not limited to just two levels—they can be three-level or even more. Only the outermost level of an arranged tensor is used to launch programs. In other words, tensors with more than two levels are hierarchical and can be indexed and iterated over within the application function.

Now, let’s implement a matrix multiplication kernel to better understand indexing and iteration in NineToothed, as well as deepen our understanding of the arrange-and-apply paradigm.

Before we begin implementation, we first need to understand the algorithm we want to realize. Here’s a diagram for the algorithm:

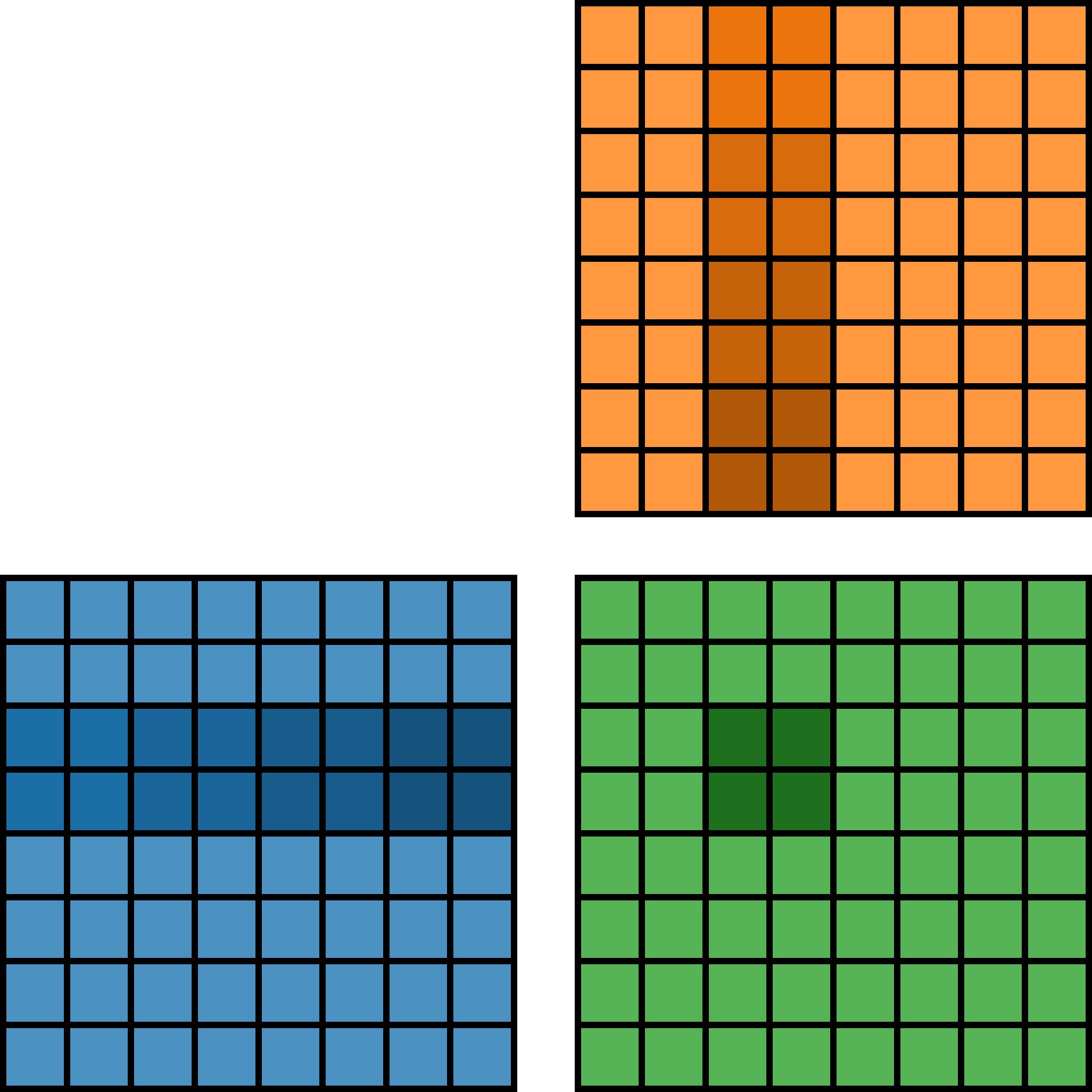
In simple terms, we tile three matrices into blocks. For each block in \(C\), we need to iterate over the corresponding row of blocks of \(A\) and the corresponding column of blocks of \(B\). Then, for each iteration, we need to perform a small matrix multiplication between the blocks of \(A\) and \(B\), and accumulate the result into the block of \(C\).

With this algorithm in mind, let’s begin the implementation, starting with the arrangement phase:

BLOCK_SIZE_M = ninetoothed.block_size()
BLOCK_SIZE_N = ninetoothed.block_size()
BLOCK_SIZE_K = ninetoothed.block_size()


def arrangement(input, other, output):
    output_arranged = output.tile((BLOCK_SIZE_M, BLOCK_SIZE_N))

    input_arranged = input.tile((BLOCK_SIZE_M, BLOCK_SIZE_K))
    input_arranged = input_arranged.tile((1, -1))
    input_arranged = input_arranged.expand((-1, output_arranged.shape[1]))
    input_arranged.dtype = input_arranged.dtype.squeeze(0)

    other_arranged = other.tile((BLOCK_SIZE_K, BLOCK_SIZE_N))
    other_arranged = other_arranged.tile((-1, 1))
    other_arranged = other_arranged.expand((output_arranged.shape[0], -1))
    other_arranged.dtype = other_arranged.dtype.squeeze(1)

    return input_arranged, other_arranged, output_arranged

In this code, we first define the symbols BLOCK_SIZE_M, BLOCK_SIZE_N, and BLOCK_SIZE_K, which represent the shapes of the blocks. We then tile output into blocks of shape (BLOCK_SIZE_M, BLOCK_SIZE_N), input into (BLOCK_SIZE_M, BLOCK_SIZE_K), and other into (BLOCK_SIZE_K, BLOCK_SIZE_N):

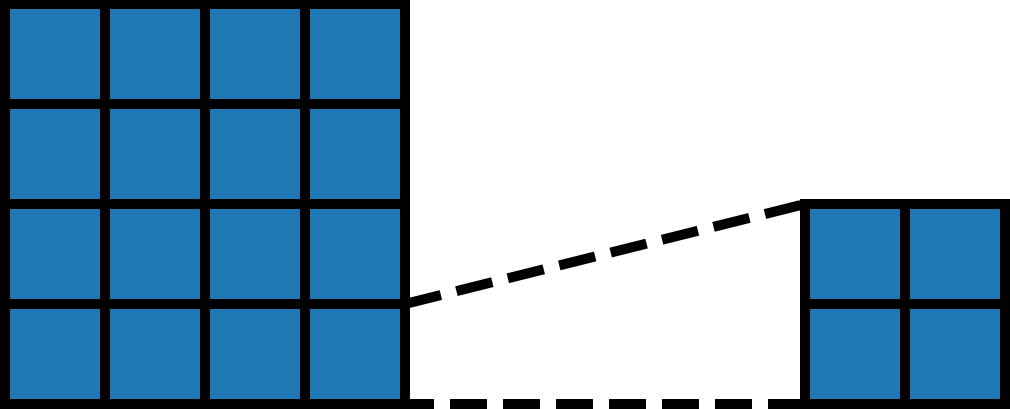
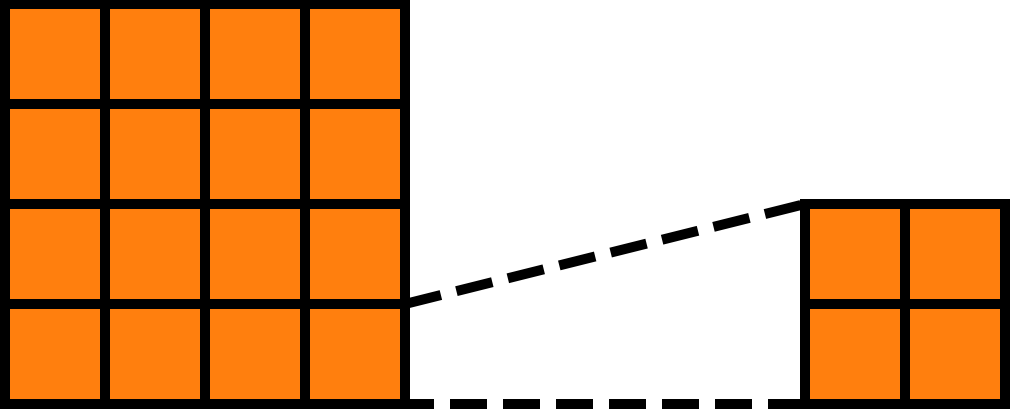
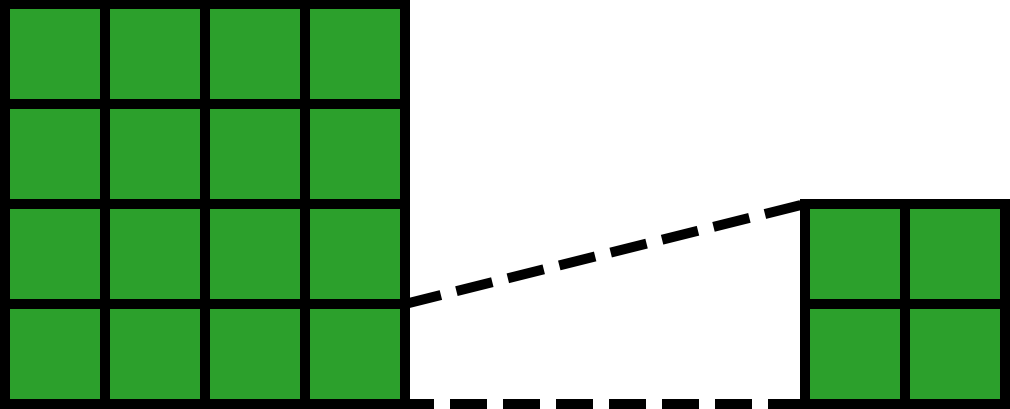
We notice that simple arrangement is not enough for matrix multiplication. According to the diagram, each block in output corresponds to a row of blocks in input and a column of blocks in other. So we need to further tile input row-wise and other column-wise:

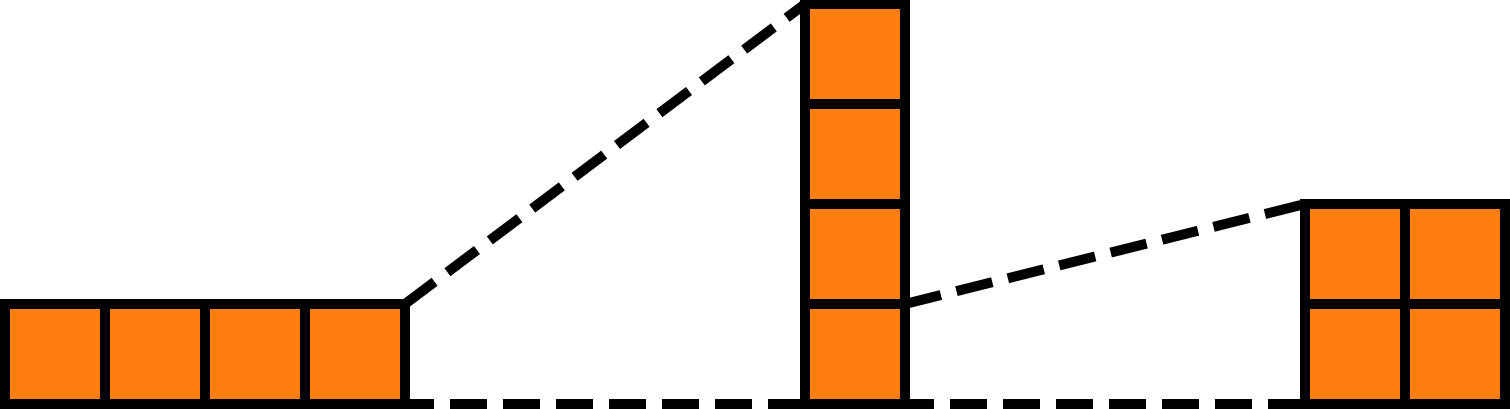
But we’re still not done. Remember how the NineToothed compiler establishes the relationship between multiple parameter tensors?

The NineToothed compiler launches programs based on the shape of the outermost tensors of the arranged parameter tensors and maps the second outermost tensors to these programs.

Why is this important? Because it implies a crucial rule: The outermost tensors of the arranged parameter tensors must have the same shape.

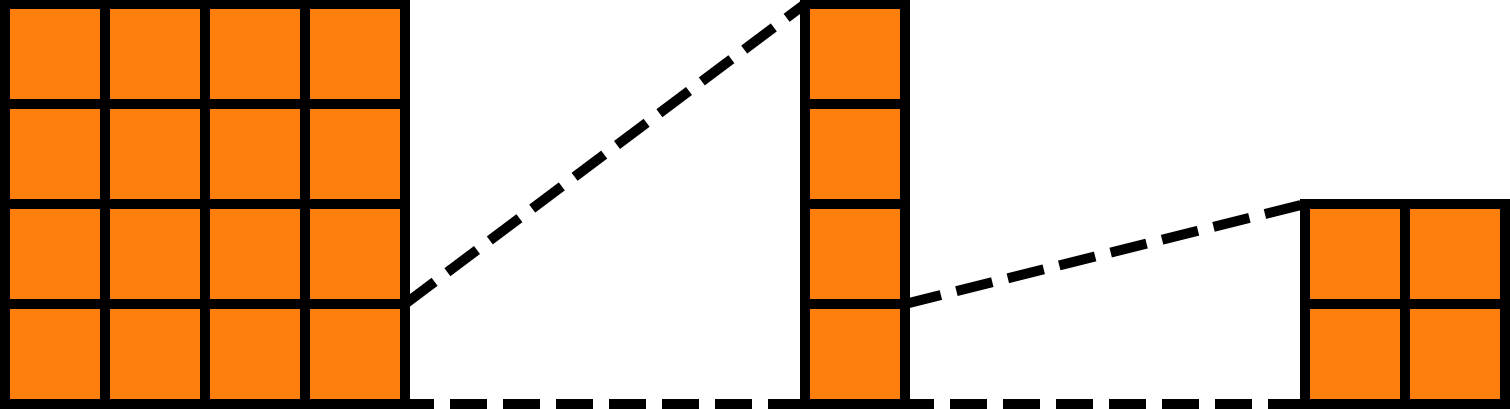
Currently, the shapes of the outermost tensors of the arranged parameter tensors are (4, 1), (1, 4), and (4, 4)—clearly inconsistent. This suggests that the arrangement is incorrect or incomplete. From the diagram, we know we need to align each row of blocks of input with each column of blocks of other. We can achieve this via expand, horizontally expanding input and vertically expanding other to match the shape of output:

Now, the outermost tensors of the arranged parameter tensors have matching shapes. Technically, arrangement is complete and we could proceed to write the application function. However, we notice that the row of blocks of input and the column of blocks of other are two-dimensional, and their shapes are of the form (1, ...) and (..., 1) respectively. In other words, if we do not perform additional operations, the way to index the row of blocks and the column of blocks would be input[0, k] and other[k, 0]. If we want to find the range of k based on input, we would need to use input.shape[1]. But we know that dimensions of size 1 can be safely removed here. That’s why we add squeeze:

With this, we can now index the row of blocks and the column of blocks with input[k] and other[k], and use input.shape[0] to determine the range of k.

At this point, the arrangement phase is complete. The final arrangement result is:

Now let’s look at the application function:

def application(input, other, output):
    accumulator = ntl.zeros(output.shape, dtype=ntl.float32)

    for k in range(input.shape[0]):
        accumulator += ntl.dot(input[k], other[k])

    output = accumulator

Within the function body, we first define an accumulator to accumulate intermediate results. Then, we iterate over the row of blocks of input and the column of blocks of other, and accumulate the results of small matrix multiplications into the accumulator. Finally, we write the accumulator into the corresponding block of output. Since this happens on each block of output, the overall matrix multiplication is completed.

Just like in the vector addition example, after defining arrangement and application, we can integrate them using ninetoothed.make to build a kernel:

kernel = ninetoothed.make(arrangement, application, (Tensor(2), Tensor(2), Tensor(2)))

The kernel can be invoked like this:

import torch

dtype = torch.float16
device = "cuda"

input = torch.tensor(((1, 2), (3, 4)), dtype=dtype, device=device)
other = torch.tensor(((5, 6), (7, 8)), dtype=dtype, device=device)

output = torch.empty((input.shape[0], other.shape[1]), dtype=dtype, device=device)
kernel(input, other, output)

reference = torch.tensor(((19, 22), (43, 50)), dtype=dtype, device=device)
assert torch.allclose(output, reference)